Window function

Window function#

The WDM transform is built around a smooth window that localizes the FFT in time while keeping good behavior in frequency (reduced leakage, approximate perfect reconstruction with sufficient overlap).

PyWavelet exposes two related objects:

  • phitilde(ω): the window in the frequency domain

  • phi(t): the window in the time domain (computed via an inverse FFT of phitilde)

In the code these live in pywavelet.transforms.phi_computer.

Sliding window intuition

What the parameters mean#

nx (called d in the implementation)#

nx controls the steepness/smoothness of the frequency-domain taper used in phitilde(ω) (via a normalized incomplete beta function).

  • larger nx → smoother/steeper transition band (often less leakage, but can broaden support)

  • smaller nx → sharper transition (can increase ringing/leakage depending on overlap)

See pywavelet.transforms.phi_vec() and pywavelet.transforms.phitilde_vec_norm().

mult (called q in phi_vec)#

mult controls the window support length in samples:

  • K = 2 * mult * Nf

This is the length of the windowed segment that is FFT’d per time bin in the time-domain implementation. More overlap (larger mult) usually improves reconstruction quality but costs more compute.

The implementation warns that the transform is only approximately exact unless overlap is sufficient (a common rule-of-thumb is mult ≈ Nt/2 when feasible).

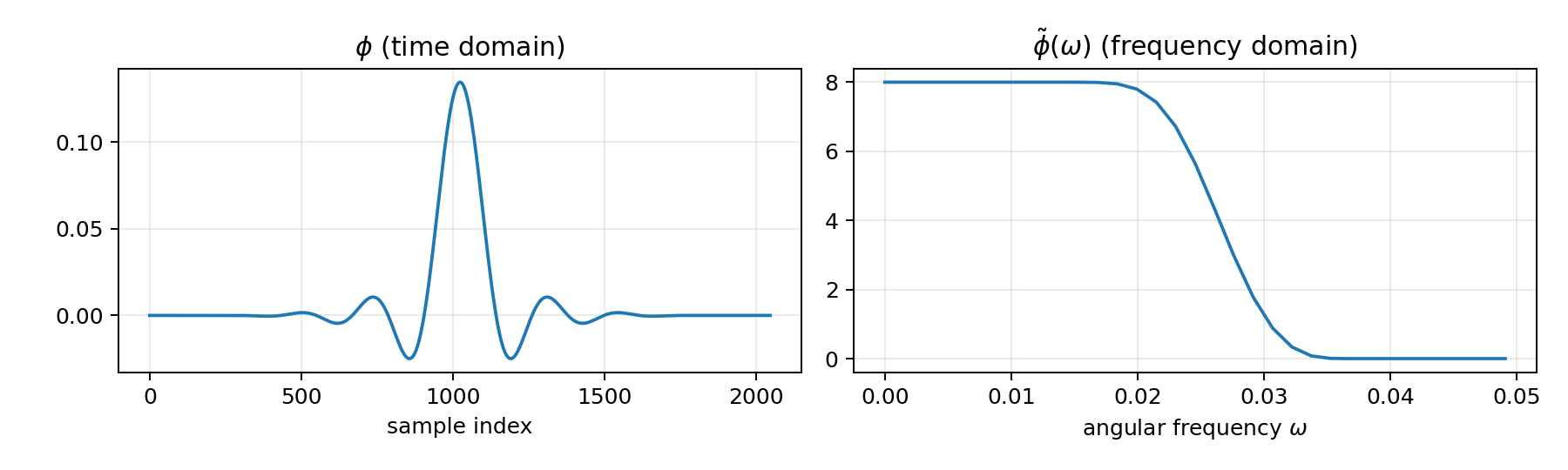
Quick visualization#

You can plot the time-domain window and the frequency-domain window samples:

import numpy as np
import matplotlib.pyplot as plt

from pywavelet.transforms import phi_vec, phitilde_vec_norm, omega

Nf, Nt = 64, 64
nx = 4.0
mult = 16

phi = phi_vec(Nf, d=nx, q=mult)
w = omega(Nf, Nt)
phitilde = phitilde_vec_norm(Nf, Nt, d=nx)

fig, axes = plt.subplots(1, 2, figsize=(10, 3))
axes[0].plot(phi)
axes[0].set_title("phi (time domain)")
axes[0].set_xlabel("sample index")

axes[1].plot(w, phitilde)
axes[1].set_title("phitilde (frequency domain)")
axes[1].set_xlabel("angular frequency ω")
fig.tight_layout()
Example plot of phi and phitilde

Common symptoms#

  • Leakage / smeared tracks in the wavelet plot: try increasing mult (and/or nx).

  • Slow runtime: reduce mult first; then reduce Nt/Nf.

For a visual comparison of how nx and mult change the window and the resulting transform, see Window effects.

Contents