How it works

PyWavelet implements the WDM (Wilson–Daubechies–Meyer) style time–frequency transform used in the gravitational-wave literature (see Citing PyWavelet).

At a high level, the transform:

1. chooses a time–frequency grid (Nt time bins and Nf frequency bins),

2. builds a smooth window function (phi / phitilde),

3. computes windowed FFT packets per time bin,

4. packs those packets into a real-valued wavelet coefficient grid.

Grids and shapes

For a time series with duration T and an Nt × Nf wavelet grid:

• delta_T = T / Nt (time-bin size)

• delta_F = 1 / (2 * delta_T) (frequency-bin spacing)

• total samples expected by the time-domain transform: ND = Nt * Nf

The wavelet coefficients are stored as a 2D array with shape (Nf, Nt):

• rows: frequency bins

• columns: time bins

Forward transform (time → wavelet)

Conceptually (see pywavelet.transforms.from_time_to_wavelet()):

• take the 1D signal (length ND),

• for each time bin, multiply a local segment by a window phi,

• FFT that windowed segment,

• pack selected frequency samples into the wavelet coefficient grid.

The parameter mult controls how wide the windowed segment is (and therefore how much overlap you get between neighboring time bins). See Window function.

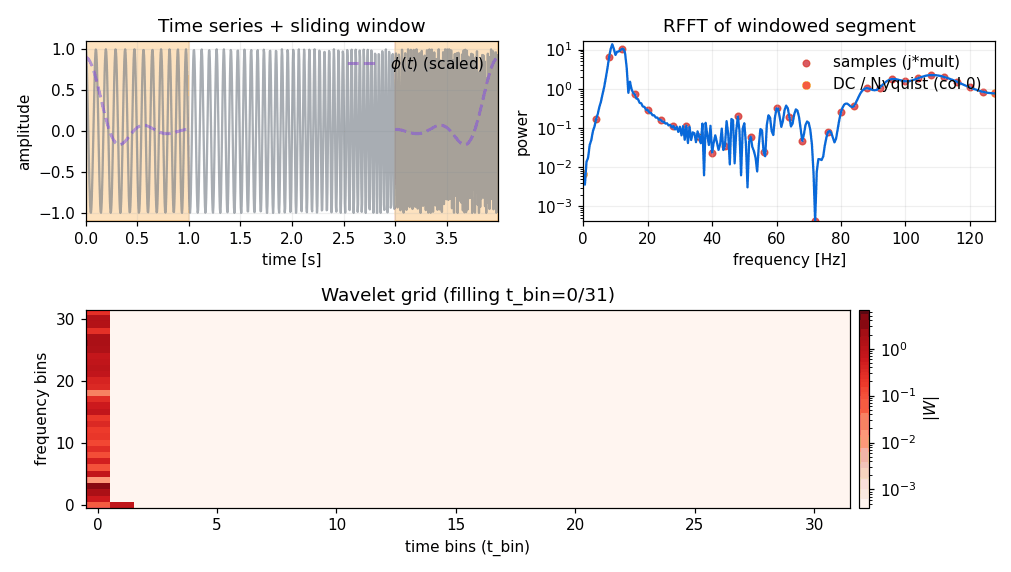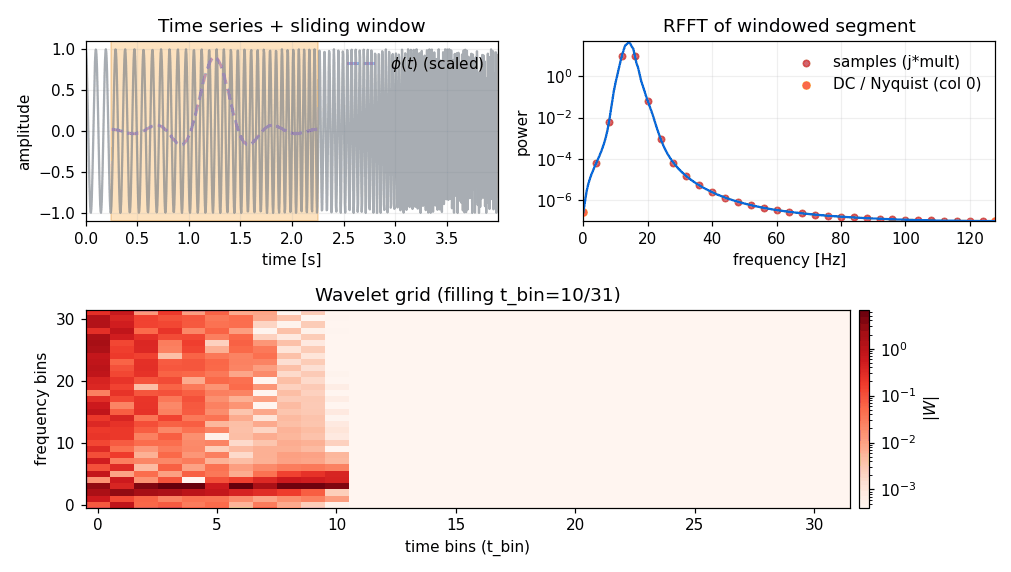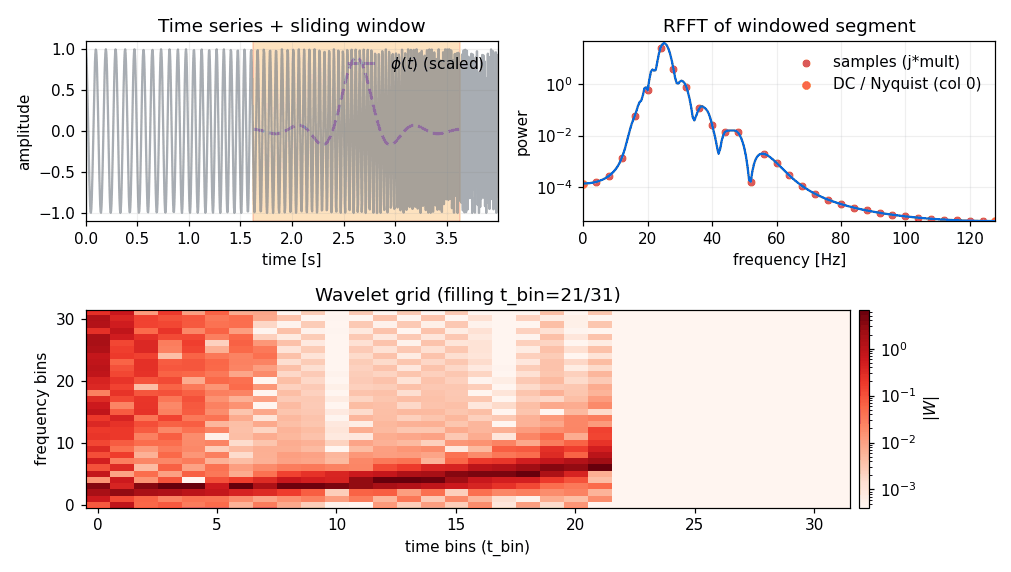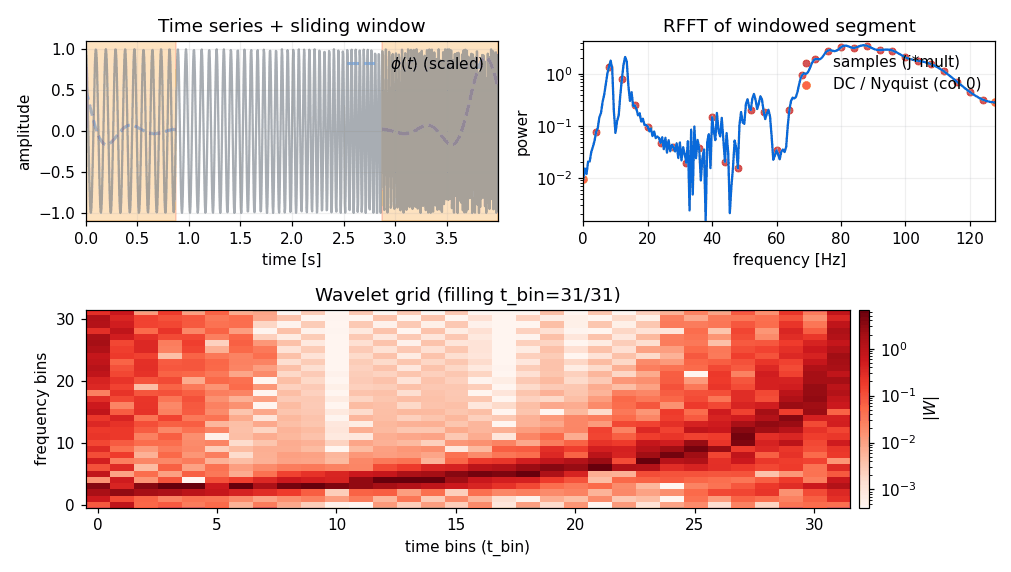
Forward transform (frequency → wavelet)

If you start from a frequency-domain series (pywavelet.transforms.from_freq_to_wavelet()), the intuition is similar:

• for each frequency bin, take a local band of frequency samples,

• taper it with phitilde,

• inverse-FFT to get a time packet,

• pack real/imag parts into a wavelet grid column using parity rules.

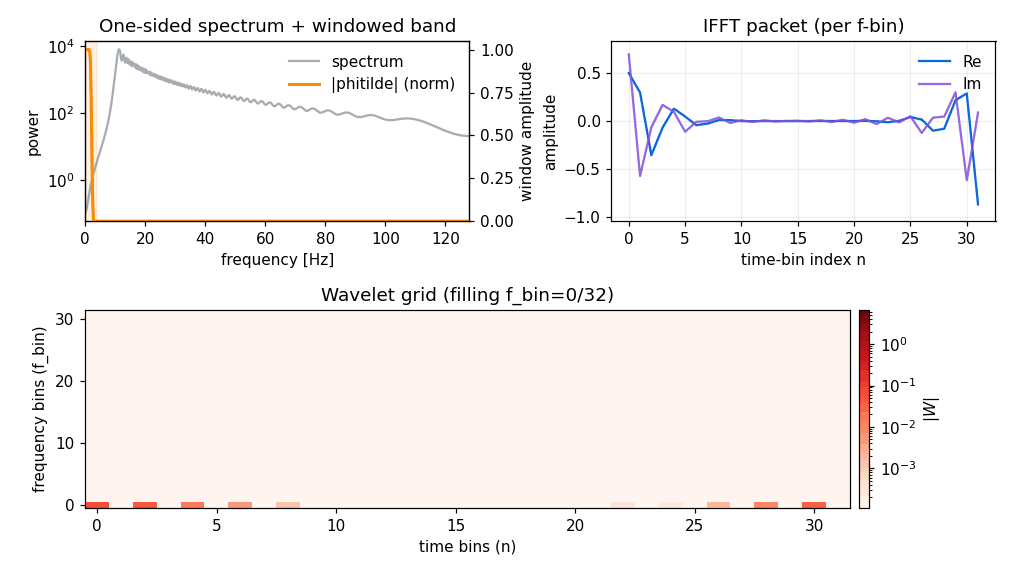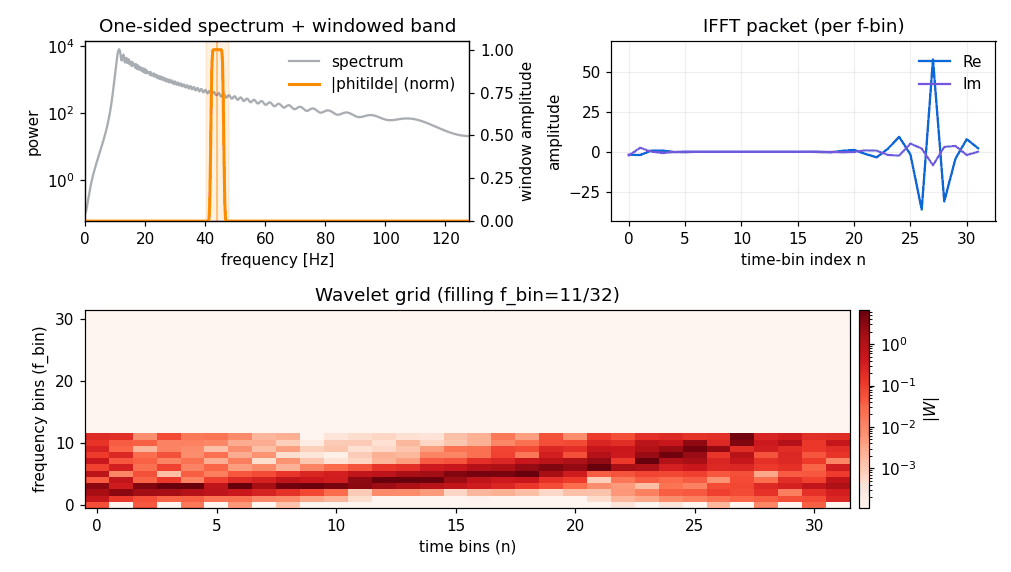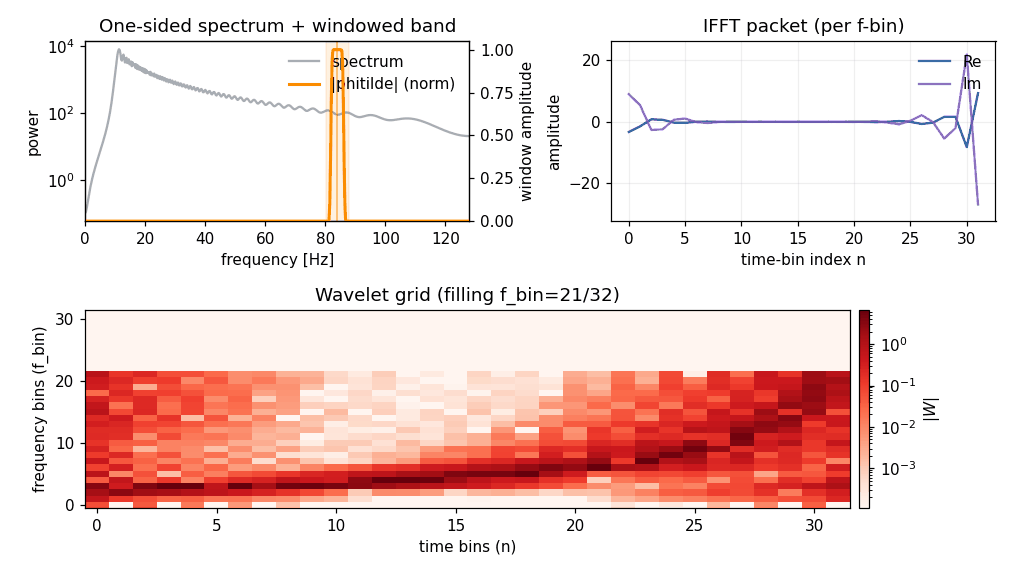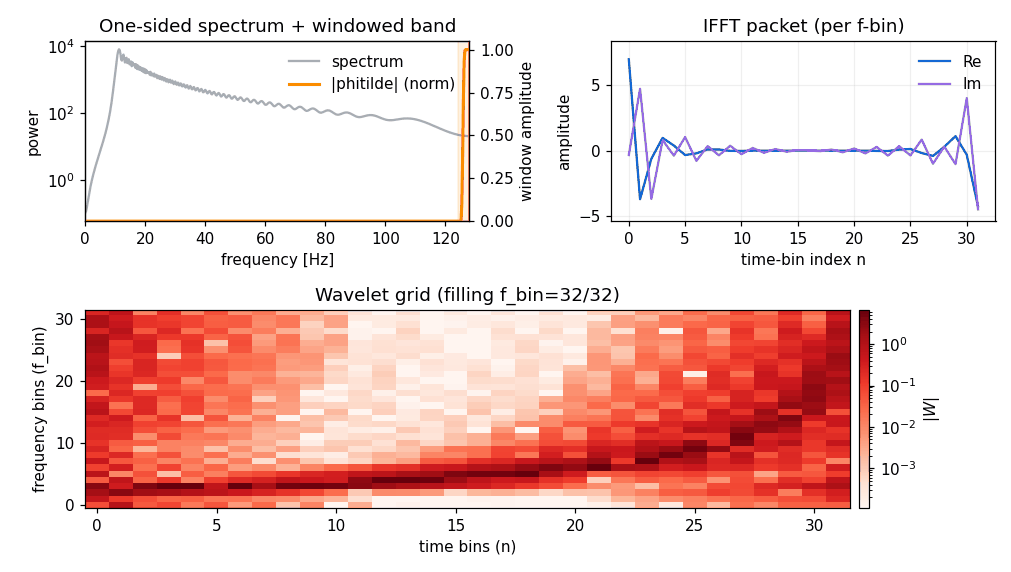
Inverse transform (wavelet → time / frequency)

The inverse does the reverse packing/unpacking and overlap-add style reconstruction:

• unpack each time bin’s packed coefficients,

• inverse FFT back to a windowed time segment,

• add the contributions back into the 1D output stream.

Where to look in the code

• Grid definitions: pywavelet.types.wavelet_bins.compute_bins()

• Window construction: pywavelet.transforms.phi_vec() and pywavelet.transforms.phitilde_vec_norm()

• NumPy implementation:

  • forward: pywavelet.transforms.from_time_to_wavelet()

  • inverse: pywavelet.transforms.from_wavelet_to_time()